
研究背景
尽管近40年前开发出了第一批对接程序,我们可以使用不同的方法(搜索算法,分为系统和随机搜索方法)来寻找和评估(评分函数,分为基于经验的、基于力场的和基于知识的函数)潜在的配体-受体配合物,但是没有一种能够适合所有情况的完美方法,所以仍需要不断开发新的对接程序并对其进行评估和验证。如果所用的对接程序不能再现参考配体的结合位姿,则不能保证其它潜在配体的结果有任何用处。
对接程序性能的评估
常见方法是计算对接和参考配体位姿之间的均方根偏差(RMSD),即两个位姿中相应原子之间的平均距离,用于确定对接程序再现正确的、最常见的晶体学位姿的能力的典型的RMSD截断值为2 Å。然而,除了对接程序本身的性能之外,这种能力可能受到晶体学数据质量(例:如果参考结构的质量差,就会有空间碰撞,缺少侧链等)、所用的RMSD算法类型(标准RMSD方法、最小距离的RMSD和对称校正的RMSD)以及存在突出于配体口袋外且不与受体分子形成任何显著相互作用的柔性取代基的影响,后者可以显著增加RMSD,但对实际结合亲和力没有明显影响;另一种方法是计算恢复的配体-受体接触的比例,这也避免了RMSD方法的缺点,但必须定义“配体-受体触点”和“恢复的配体-受体触点”的长度截断值。确定配体-受体接触的另一种方法是使用AlteQ方法。
本文使用量子自由轨道AlteQ方法来评估配体结合位姿及其排序的正确性。由于配体和受体之间的相互作用遵循最大互补性原则,因此通过用AlteQ方法计算二者空隙中的电子密度,可以获得描述这些相互作用互补性的方程。与配体RMSD方法相比,AlteQ方法可以更好地评估配体和受体之间的接触质量,因此其被认为是“恢复配体-受体接触的部分”方法的改进。
量子自由轨道AlteQ方法
该方法基于使用斯莱特的原子类型贡献,计算配体和受体之间空隙中的电子密度。由于所有配体-受体相互作用都由电子云的重叠决定,且遵循最大互补性原则,AlteQ方法可不必强加任何任意的截断值。如方程(1)所示。
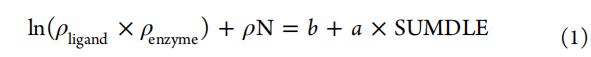
其中b和a是方程的参数,参数b无量纲,参数a以Å-1为单位,ρligand表示配体对分子空间第三点电子密度的贡献,ρenzyme表示受体对同一点电子密度的贡献。AlteQ方法可以用来计算配体−受体的接触,而无需施加任何任意的切断,而仅仅依赖于原子电子云的大小。通过识别对第m点电子密度贡献最大的配体和受体原子及其与该点的距离(SUMDLE),可以识别和量化最重要的配体-受体相互作用。这反过来可以提供关于配体-受体结合亲和力的有价值的信息。
结果
1. 晶体复合物和能量最小化复合物的比较
对于本文研究的三种体系(CDK2、HIV-1蛋白酶和乙酰胆碱酯酶)中的每一种被研究的体系,都获得了7种复合物构象(晶体复合物构象、5种对接的复合物构象和能量最小化后的复合物构象),每一种复合物的最小化构象被作为参考构象。表1总结了三种研究体系的RMSD值。为限制搜索量,对接消耗故意设置得不很高,能量范围设为4。目的是确保找到除全局最小值以外的其他配体构象并保留这些构象,从而测试算法的性能。
表1. 晶体结构和对接的配体-受体构象与它们对应的能量最小化构象的RMSD值
表格来源于JCIM

基于使用AlteQ方法获得的数据,使用等式1获得所有复合物的回归线(表2)。图1a为最小化复合物3SW7的例子。红色的回归线(最小的3SW7复合物)和绿色的回归线(所有最小的CDK2复合物的平均值)实际上是重叠的。这适用于所有最小化复合物,与配体结构无关,这表明它们与结合位点形成非常相似的相互作用。1B39复合物包含在平均系数的计算中,如图1b所示。此外,可以看到1B39复合体是唯一SUMDLE值低于2.5 Å的复合体。对于晶体复合物和最小化复合物,这些系数的值基本相同,但晶体复合物的标准差更高。
表2. 晶体结构和其对应的能量最小化配体-受体构象的b和a系数的值
表格来源于JCIM

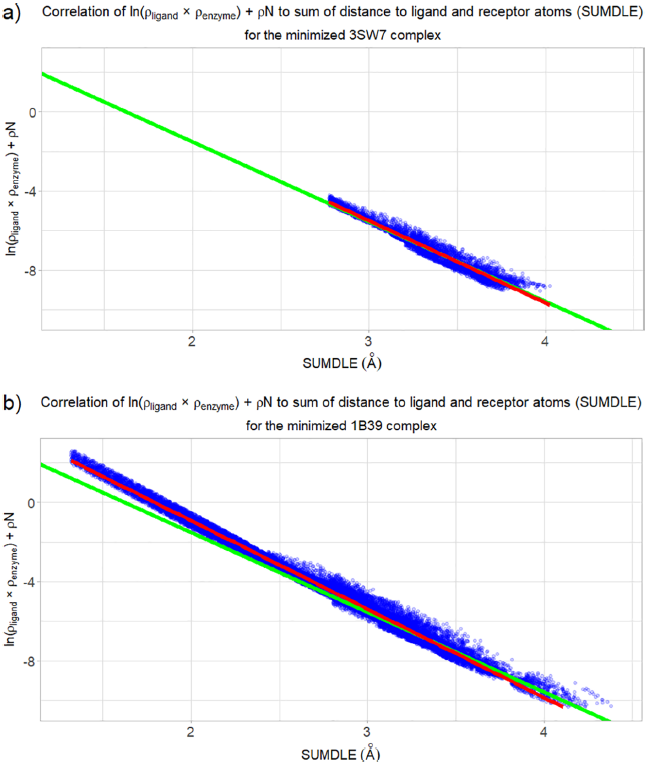
图1. ln(ρligand × ρenzyme)和ρN之和与能量最小化复合物中任一点到最高贡献的配体和酶原子的距离之和(SUMDLE)的相关性
图片来源于JCIM
2. 对接复合物和能量最小化复合物的比较
对于对接的复合物,情况则完全不同。有一些复合物的系数b和a的值与平均值相似,但大多数复合物的回归线明显不同。在图2中,可以看到能量最小化的4FKO_ver_2复合物与最佳对接的4FKO_ver_2复合物的比较(该复合物的对称性校正后的RMSD为0.432 Å,是所有对接的CDK2复合物中RMSD最低的复合物)。最小化的4FKO_ver_2配合物的回归线实际上与“正确的”回归线相同,而最佳对接配合物的回归线非常不同。另外,对接的复合物缺乏所有短于3.3 Å的配体-受体相互作用。图3叠合了的能量最小化和最佳对接的4FKO_ver_2复合物,在结合口袋内具有几乎相同的构象。由于最强的配体-受体相互作用可以忽略,仅根据RMSD分数来估计对接精度可能会产生误差。将配体-受体相互作用分析完全建立在对接结果的基础上同样也会出错。要提高对接结果准确性,就要对复合物进行几何优化,这允许恢复一些配体-受体相互作用,代价是计算时间较长。图4和图5分别对能量最小化复合物和最佳对接复合物进行了可视化分析,发现相互作用的模式完全不同,配体和受体电子云之间的重叠较少,这再次证实了对接过程中尽管能够获得与正确位姿非常相似的位姿,但可能会忽略重要的相互作用及其平衡距离。
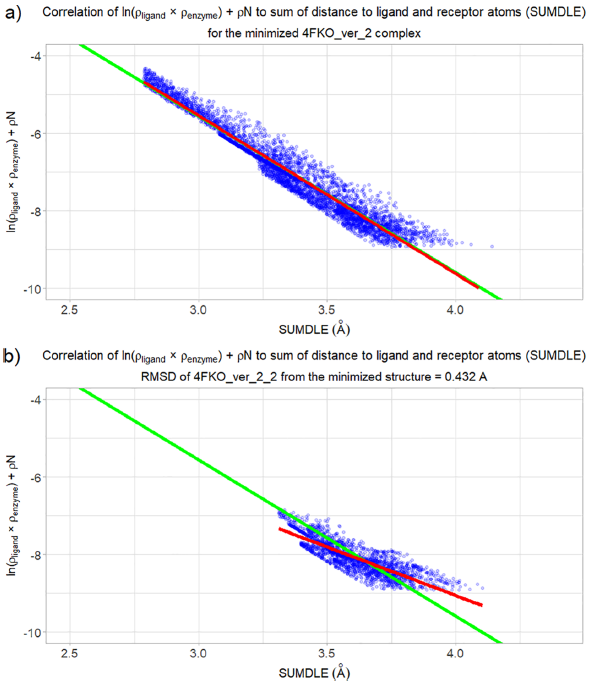
图2. ln(ρligand × ρenzyme)和ρN之和与能量最小化复合物中任一点到最高贡献的配体和酶原子的距离之和(SUMDLE)的相关性
图片来源于JCIM
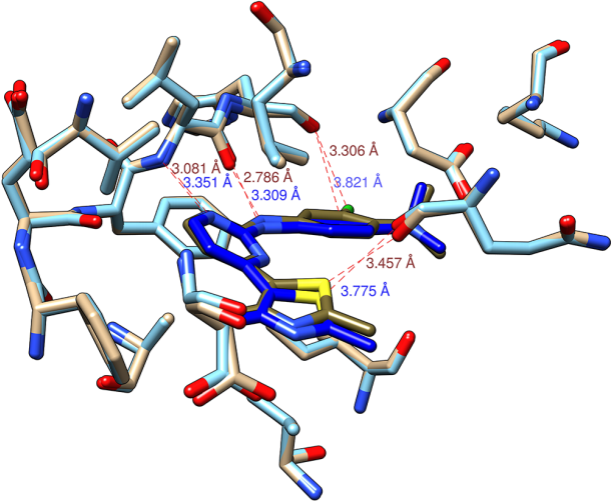
图3. 能量最小化(棕色和褐色)和最佳对接(深蓝和浅蓝)的4FKO_ver_2复合物的叠合
图片来源于JCIM
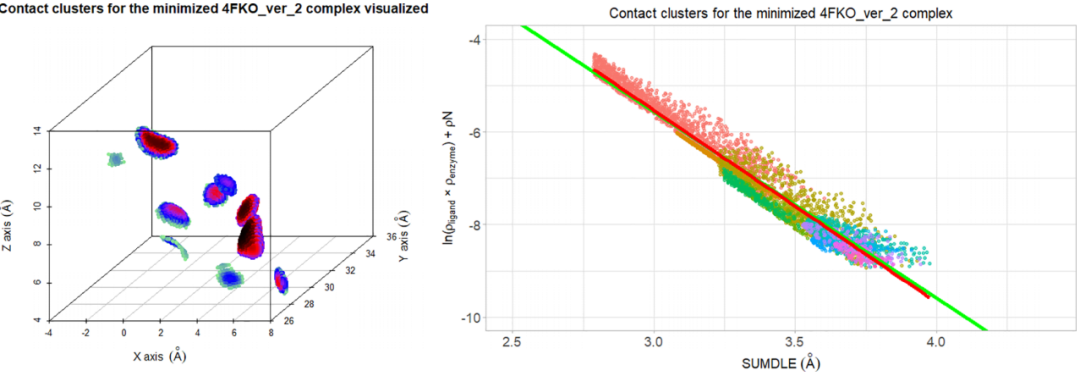
图4. 能量最小化的4FKO_ver_2复合物的可视化
图片来源于JCIM
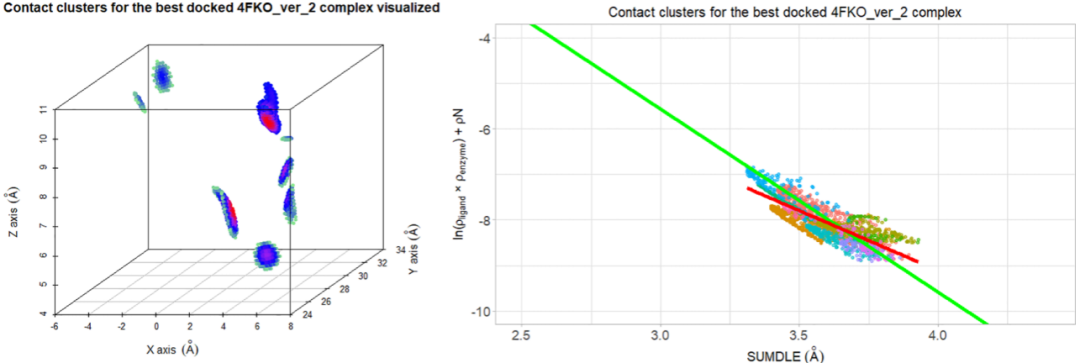
图5. 最佳对接的4FKO_ver_2复合物的可视化
图片来源于JCIM
与具有较低RMSD的配体相比,一些具有较高RMSD的对接配体可以更好地保持与受体原子的相互作用,如图6a中能量最小化的复合物3SW7,图6b中最佳对接的3SW7复合物(3SW7_2,RMSD是0.667的能量最小化的复合物)和图6c中的复合物3SW7_4(RMSD是2.416的能量最小化的复合物)。从图6的左右侧可以看出,尽管3SW7_2复合物的RMSD较低,但能量最小化的复合物在3SW7_4中配体-受体的接触比在3SW7_2中的接触更多。
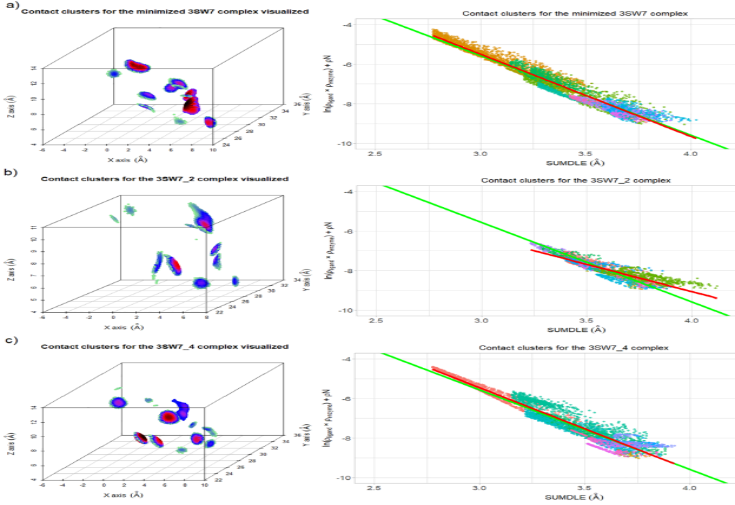
图6. 3SW7配合物在三维空间中的接触集
图片来源于JCIM
3. PDBbind核心集复合物的比较
图7中对接复合物的回归线比能量最小化复合物的回归线分散得多,这表明对接化合物的结合亲和力范围比预期的更大。图8显示了所有1400个测试构象的斜率和截距系数b和a之间的相关性,显然,对接配合物有更大范围的系数b和a,而能量最小化的和晶体复合物倾向于聚集在一起,除了较小的配体(分子碎片),其斜率系数往往为>-3.5此外,正如前面讨论的三个系统,斜率和截距系数之间的相关性非常高,调整后的R2= 0.9952。这证实了AlteQ方法是一种稳健的方法,可以应用于各种配体-受体复合物。
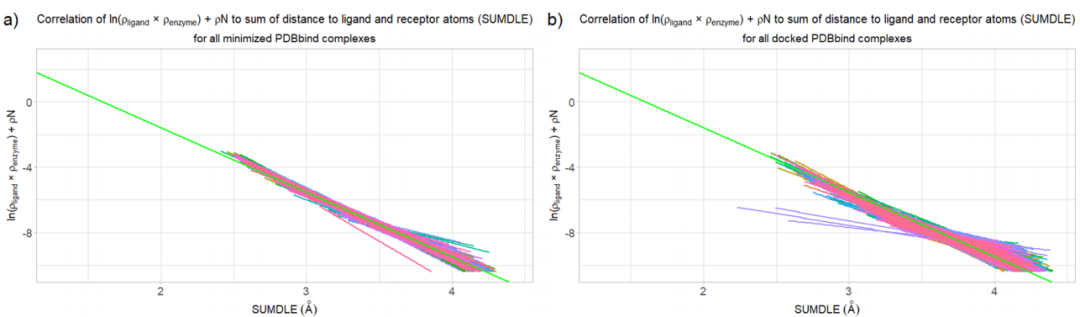
图7. ln(ρligand × ρenzyme)和ρN与(a)能量最小化和(b)对接测试的PDBbind中的复合物中的任一点到最高贡献配体和酶原子的距离之和(总和)与相应的平均回归线(绿色显示)的相关性
图片来源于JCIM
图8. 所有测试的PDBbind核心集复合物的斜率和截距系数的相关性。对接的复合物显示为蓝色,能量最小化的复合物显示为绿色,晶体复合物显示为红色
图片来源于JCIM
4. RMSD对于评价配体-受体对接优劣存在缺陷
本研究表明使用RMSD作为评估对接优劣不具有较优的有效性,因为较高的RMSD并不一定与关键蛋白-配体相互作用的变化相对应。RMSD作为一个标量,是分子中所有原子位置变化的平均值,不提供任何关于位置变化类型的信息(如平移或旋转),或者分子的哪些部分排列整齐,哪些没有。在计算蛋白质的RMSD时,灵活性问题更为突出,这在配体对接中也很重要,特别是当部分配体位于结合口袋外时。相反,确定结合位姿正确性的另一种方法是使用恢复的配体-受体接触的部分,AlteQ方法。该方法采用对接和参考配合物之间的截断距离和距离差,使用的截断值不同,结果可能也不同。使用AlteQ方法进行对接可以通过定义和计算配体和受体原子之间的接触强度来提高准确性,并基于它们的电子云重叠、大型生物分子系统的电子密度的拓扑分析、物理化学性质和生物活性进行评估。这样,就可以得到配体-受体相互作用的最佳方程,而对接位姿需要满足这个方程才能认为其是正确的。
RMSD的计算有几种不同的方法:
(1) 标准RMSD方法是固定的一对一对应,它不考虑分子的对称性和等效原子的存在。例如,异丙基旋转180°将产生两种不同的RMSDs,尽管这两种结构是等价的。这导致了对真实RMSD的高估;
(2) 最小距离RMSD方法,测量同一类型原子之间的距离,但在某些情况下可能不强制一对一的原子对应,就像AutoDock 和Vina所采用的那样,一些原子可以被多次用于RMSD计算,而其他原子可以被忽略,从而导致对真实RMSD的低估;
(3) 在DOCK中使用的对称性校正RMSD方法,考虑了分子的对称性,调整了原子对原子的对应关系,所有原子都被用于计算。这样,获得的RMSD值总是等于或低于标准RMSD获得的值。然而,这种方法在计算“正确”构象和对接构象之间的对应关系时也存在缺陷,因为它没有包括分子灵活性和配体-受体相互作用的信息。
结论与展望
由于验证对接结果的RMSD标准有其缺陷,因此也正在开发评估结果正确性的替代方法。 通过上述三种比较发现,AlteQ程序更适合于对配体-受体相互作用和靶向对接的深入分析,而不是针对常规虚拟筛选任务进行优化。与经典方法相比,AlteQ方法的优势在于它没有使用任意截断值,而是直接从配体和受体原子的电子密度来计算它们之间的接触强度,从而确定配体和受体之间最重要的相互作用和对应于结合常数的系数a。它代表了一种基于电子云重叠确定配体-受体相互作用的替代方法,可对同一配体的不同对接位姿进行排序,同时确定与受体之间最强的相互作用。然而由于系数a与配体结合亲和力相关,其被用于排列配体位姿和预测其结合常数的用途也正在研究中。
工具下载地址
AlteQ: www.chemosophia.com
参考文献
Hrvoje Rimac, Maria Grishina, and Vladimir Potemkin, Use of the Complementarity Principle in Docking Procedures: A New Approach for Evaluating the Correctness of Binding Poses, Journal of Chemical Information and Modeling, 2021, 61, 4, 1801-1813. DOI: 10.1021/acs.jcim.0c01382.