背景介绍
生物大分子功能依赖于发生在不同时间尺度上的耦合过程,对这种系统的理论描述具有一定挑战性。对于蛋白质来说,折叠发生在微秒到数分钟甚至数小时的范围内,涉及到亚皮秒的键振动和水合运动。对于经典的相互作用多体系统动力学,严格的处理是基于刘维尔方程,并采用投影算子形式积分除一个或几个反应坐标外的所有自由度。对于感兴趣的可观测物,动力学通常用很少的方程来描述而不是采用一个N个粒子系统的所有位置和动量的6N个运动方程。这个粗粒化过程从确定性的哈密顿量引出了广义朗之万方程(GLE)的随机描述,对于一维坐标q(t)的情况,表示为:
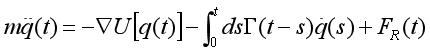
(1)
m是坐标q的有效质量。平均力场U(q)对应蛋白质的折叠自由能图景,是通过平衡概率分布ρ(q)通过U(q)=−kBTln ρ(q)得到的,其中kBT是热能,kB是波尔兹曼常数,T是绝对温度。自由度的消除引入了记忆函数Γ(t)的非马尔可夫效应,该函数描述了随时间变化的摩擦,从而将当前的动力学与过去的状态耦合起来,以及随机力FR(t)的随机效应。在平衡时,随机力FR(t)通过波动-耗散定理
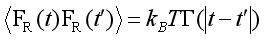
与Γ(t)相关。公式1中GLE的推导依赖于几个近似。因此,对于给定的反应坐标是微观坐标的非线性函数,不能保证公式1的有效性。
通过模拟可以直接得到的折叠自由能U(q)也可以从单分子实验中得到。但是,实验观察到的反应坐标不能保证是一个好的反应坐标。为了有效描述蛋白质折叠模拟,作者提出了不同的反应坐标。作为一种替代连续反应坐标的方法,马尔可夫模型用一组亚稳态描述蛋白质动力学,对于这组亚稳态,通常需要完全访问底层的微观坐标。这类方法都寻求最小化记忆效应的描述,以便应用随机马尔可夫理论。
在相反的方向上,人们开发了各种方法来从给定反应坐标的时间序列数据中提取记忆函数Γ(t),但由于GLE的复杂性,特别是非线性蛋白质折叠自由能与数字决定的记忆功能的结合,阻止了GLE对蛋白质折叠时间的预测。这就是为什么在蛋白质折叠理论中,主要使用马尔可夫朗之万方程(LE),其中记忆积分被瞬时摩擦项取代。这种马尔可夫理论为蛋白质折叠动力学提供了许多有用的见解,并在转换路径时间和平均折叠时间的比较中达到了高点。然而,自由能折叠理论在马尔可夫水平上的成功部分依赖于摩擦这一事实,它决定克雷默折叠时间的前因子,通常被用作拟合参数。即使允许摩擦随反应坐标变化并从模拟中提取,它通常也是根据折叠或重新配置时间计算的,这是通过构造实现动力学的自洽预测。事实上,最近的实验表明,直接测量的自由能势垒高度与由转换路径和折叠时间推断的高度存在显著的不一致,这可能是由于记忆效应引起的。当反应坐标的摩擦不适合折叠时间,而是直接从模拟轨迹中提取并在马氏理论框架中使用时,也会得到同样的不一致性。
主要内容
德国柏林自由大学的Roland R. Netz团队提出了一个新方法,不是寻找一个好的反应坐标,而是使用一个由原生接触的分离之和组成的标准一维坐标。相关的研究成果以 “Non-Markovian modeling of protein folding” 为题发布在国际著名期刊Proceedings of the National Academy of Sciences of the United States of America上。
作者使用精确的工具从分子动力学(MD)模拟水中螺旋形成的多肽Ala9中提取GLE的所有参数。接着在基于天然氢键距离和的一维反应坐标的α-螺旋形成多肽丙氨酸9的分子动力学(MD)模拟中,研究者提取了广义朗之万方程(GLE)的两个组成部分——折叠自由能场和随时间变化的摩擦函数。自由能U(q)显示出由低势垒分隔的多次极小值,表明螺旋的顺序形成,而多指数记忆函数Γ(t)最长衰减时间与展开时间的顺序相同。这些特性使Ala9成为一个非常敏感的动力学理论测试物。研究者用马尔可夫嵌入技术模拟得到了GLE,通过对平均折叠和展开时间的MD和GLE结果的比较,研究者证明了一维GLE是一种准确实用的描述蛋白质折叠动力学的工具。
另一方面,只要摩擦不是一个拟合参数而是从MD模拟中提取的参数,则过阻尼GLE的马尔可夫版本就不能描述肽的折叠和展开动力学。正如Grote-Hynes理论所预测的那样,记忆通常会加速势垒穿越,其中加速度大小主要取决于记忆时间的比例以及反应坐标空间中最小值与势垒之间的距离。这种由记忆引起的折叠和展开加速在反应坐标空间中伴随着明显的异常扩散。研究者的结果被系统的克雷默-莫亚尔系数(KMC)分析所证实,该分析表明高阶四次KMC是不可忽略的,线性和二次KMC在短时间内消失,正如预期的非马尔可夫效应的存在。这意味着,用福克-普朗克方程描述蛋白质折叠只在需要适当选择的特定时间尺度上有效。研究者还发现,当使用马氏模型描述非马氏蛋白质动力学时,会出现虚假的反应坐标依赖的摩擦分布。
从数值积分得到的GLE的折叠和展开时间与MD的结果吻合较好,证明了基于GLE的非马尔可夫模型的稳健性。相比之下,马尔可夫模型不能准确地描述肽动力学,特别是,即使使用空间依赖的摩擦轮廓,也不能同时再现折叠和展开动力学。研究者的方法原则上适用于任何反应坐标,也适用于单分子实验的实验轨迹。该研究结果表明,蛋白质折叠动力学的一致描述必须考虑记忆摩擦效应。
MD和GLE模拟的对比
GLE的数值积分直接通过马尔可夫嵌入实现。在图1A中,研究者展示了展开时平均首次通过时间τMFPT(qS, qF)的分布(起始位置qS=qL=0.32 nm;实线)和折叠动力学(起始位置qS = qR =0.99 nm;折线)作为最终位置qF的函数。MD和GLE模拟结果(蓝色线和橙色线)吻合得很好;这表明基于GLE的蛋白质折叠非马尔可夫模型是可行和准确的。甚至GLE和MD模拟的首次通过时间分布,都得到了令人满意的一致性。
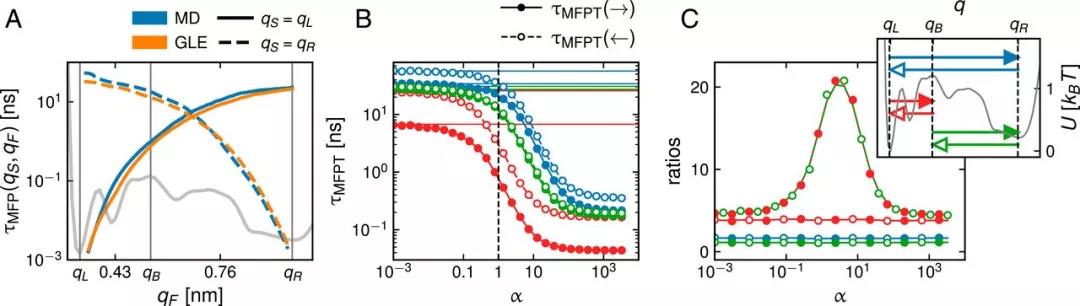
图1. 相关模拟数据。表格来源于PNAS
摩擦效应
为了证明图2B中的摩擦轮廓的局限性,研究者在图2C中显示了γunf(q)(实心圆)和γfoll(q)(空心圆)计算的MFPT折叠和展开轮廓。通过构造,使用γunf (q)的MFPTs再现了展开模拟数据,而使用γfoll(q)的MFPTs再现了折叠模拟数据。相比之下,使用γunf(q)的MFPTs不能再现模拟的折叠时间,使用γfoll (q)的MFPTs不能再现模拟的展开时间,特别是当折叠/展开时间小于10 ns时。相反,GLE模型(虚线)再现了折叠和展开MD动力学(实线)。这就强调了用马尔可夫模型来描述完全的折叠/展开动力学是不一致的。
图2. 摩擦效应相关的研究。表格来源于PNAS
结论总结
本文通过从显式水分子动力学模拟中提取多肽Ala9的时间依赖性摩擦,证明所得到的GLE模型可以直接进行数值积分,非常准确地再现了分子动力学模拟的折叠和展开动力学。该发现并不局限于基于天然氢键间距离之和的反应坐标。在保持摩擦系数(即记忆函数积分)不变的情况下,减小GLE中的记忆时间,折叠和展开事件的折叠动力学发生了显著变化。这表明记忆效应甚至对单个α-螺旋的形成动力学也很重要。
参考文献
Cihan Ayaz, Lucas Tepper, Florian N. Brünig, Julian Kappler, Jan O. Daldrop, Roland R. Netz, Non-Markovian modeling of protein folding, Proceedings of the National Academy of Sciences Aug 2021, 118 (31) e2023856118; DOI: 10.1073/pnas.2023856118.